REVIEW
林卉家 巫伊璐 戴瑢溱
1
Stack / Queue
2
Vector / Deque
3
Greedy
5
Dynamic programming
4
Structures
6
空間複雜度 / 時間複雜度
Stack / Queue
- 資料結構
- 後進先出(LIFO, Last-In-First-Out)
- 需引入函式庫<stack>


Stack



疊盤子
疊書本
疊熊熊(?
每個人都插隊
Stack
| stack <型態> 名稱 | 宣告 |
| push(元素) | 放入元素 |
| pop() | 刪除第一個元素 |
| top() | 讀取最上面的元素 |
| empty() | 是否為空 |
| size() | 內有幾個元素 |
Stack

Data2.push(名稱)
Data2.pop()
Data2
Stack
#include <iostream>
#include <stack>
using namespace std;
int main(){
stack <int> s;
for(int i=1;i<=10;i++){
s.push(i);
}//s=[1,2,3,4,5,6,7,8,9,10]
int m=s.size();
for(int i=0;i<m;i++){
cout<<s.top()<<endl;//依序讀取10,9,8...,1
s.pop();//依序刪10,9,8...,1
}
cout<<s.size()<<"個元素"<<endl;//全部刪光剩0個元素
return 0;
}- 資料結構
- 先進先出(FIFO, First-In-First-Out)
- 需引入函式庫<queue>

Queue

排隊
Queue
| queue <型態> 名稱 | 宣告 |
| push(元素) | 放入元素 |
| pop() | 刪除第一個元素 |
| front() | 讀取最前面的元素 |
| empty() | 是否為空 ( 空: 1 / 有元素: 0) |
| size() | 內有幾個元素 |


Data1.push()
Queue

Data1


Queue

queueData.pop()
Data1
Queue
#include <iostream>
#include <queue>
using namespace std;
int main(){
queue <int> q;
for(int i=1;i<=10;i++){
q.push(i);
}//q=[1,2,3,4,5,6,7,8,9,10]
int m=q.size();
for(int i=0;i<m;i++){
cout<<q.front()<<endl;//依序讀取1,2,3,...,10
q.pop();//依序刪1,2,3,...,10
}
cout<<q.size()<<"個元素"<<endl;//全部刪光剩0個元素
return 0;
}Vector / Deque
宣告與初始化
// 空的 vector
vector<int> v1;
// 容量為 5,元素預設為 0
vector<int> v2(5);
// 容量為 5,每個元素都初始化為 100
vector<int> v3(5, 100);
// 列表初始化
vector<int> v4 = {1, 2, 3, 4, 5}; 宣告與初始化
// 空的 vector
vector<int> v1;
// 容量為 5,元素預設為 0
vector<int> v2(5);
// 容量為 5,每個元素都初始化為 100
vector<int> v3(5, 100);
// 列表初始化
vector<int> v4 = {1, 2, 3, 4, 5}; vector<int> v;
// 新增元素(尾部)
v.push_back(10);
v.push_back(20);
v.push_back(30);
// 刪除尾部元素
v.pop_back();
// 插入元素
v.insert(v.begin() + 1, 15);
// 刪除指定位置的元素
v.erase(v.begin());
// 清空整個 vector
v.clear();
// 獲取元素數量
cout << "當前元素數量: " << v.size() << endl;
// 獲取最大容量
cout << "最大容量: " << v.capacity() << endl;
// 存取元素
if (!v.empty()) {
// 使用索引存取
cout << "第一個元素: " << v[0] << endl;
// 使用 at() 存取
cout << "第二個元素: " << v.at(1) << endl;
} else {
cout << "vector 目前為空,無法存取元素。" << endl;
}基本操作
deque<int> dq; // 宣告一個空的
// 插入元素
dq.push_back(10); // [10]
dq.push_front(20); // [20, 10]
dq.push_back(30); // [20, 10, 30]
// 訪問元素
cout << "第一個元素: " << dq.front() << endl; // 20
cout << "最後一個元素: " << dq.back() << endl; // 30
cout << "第二個元素: " << dq[1] << endl; // 10
// 刪除元素
dq.pop_front(); // [10, 30]
dq.pop_back(); // [10]
// 判斷是否為空
if (dq.empty()) {
cout << "Deque 是空的" << endl;
} else {
cout << "Deque 長度: " << dq.size() << endl;
}deque
| vector | deque | |
|---|---|---|
| 插入元素 | push_back() | push_back(), push_front() |
| 刪除元素 | pop_back() | pop_back(), pop_front() |
| 訪問元素 | operator[], at() | operator[], at() |
| 元素量 | size() | size() |
| 是否為空 | empty() | empty() |
| 訪問首尾 | front(), back() | front(), back() |
| 最大容量 | capacity() | X |
compare
push_back(10)
10
push_front(20)
10
20 10
push_back(30)
20 10
20 10 30
dq.push_back(10);
dq.push_back(20);
dq.push_front(30);
cout << dq.front() << endl;
cout << dq.back() << endl;
cout << dq[1] << endl; dq.push_back(10);
dq.push_back(20);
dq.push_front(30);
cout << dq.front() << endl;
cout << dq.back() << endl;
cout << dq[1] << endl; 30 20 10
pop_back()
20 10 30
20 10
pop_front()
20 10
10
dq.push_back(10);
dq.push_back(20);
dq.push_front(30);
cout << dq.front() << endl;
cout << dq.back() << endl;
cout << dq[1] << endl;
dp.pop_front();
dp.pop_back();
if (dq.empty()) {
cout << "Deque 是空的" << endl;
} else {
cout << "Deque 長度: " << dq.size() << endl;
}dq.push_back(10);
dq.push_back(20);
dq.push_front(30);
cout << dq.front() << endl;
cout << dq.back() << endl;
cout << dq[1] << endl;
dp.pop_front();
dp.pop_back();
if (dq.empty()) {
cout << "Deque 是空的" << endl;
} else {
cout << "Deque 長度: " << dq.size() << endl;
}1
vector內存使用少
deque比vector更適合頻繁push_front()
比list更適合隨機存取
常用於滑動視窗、BFS搜索
〞
Greedy
- 反覆執行某個任務
- 找當下最優解
貪婪演算法Greedy
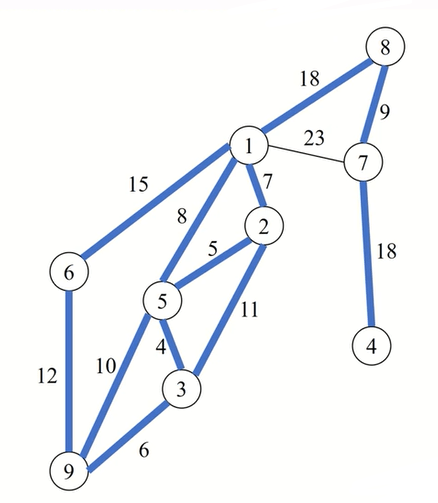
最短路徑⚠️
刪數字
1 2 3 5 6
Greedy-刪數字
4 2 9 1 3 9 6
刪4個數字變最小
4 2 9 1 7 9 6
4 2 9 1 7 9 6
4 2 9 1 7 9 6
4 2 9 1 7 9 6
剩下2 1 6
Greedy-不適用於最短路徑
指令:連通所有點
任務:挑一個最短路線鋪道路
a
b
c
d
5
6
7
11
9
e
10
~9其實不需要~
Structures
public
private
class zsisc {
public:
string name;
int height;
}class zsisc {
private:
string name;
int mathScore;
}該類別內外皆可存取
外部程式可直接存取、修改
只能在該類別內存取
外部程式無法直接存取,必須用公有函式存取
public
private
class zsisc {
public:
string name;
int height;
}class zsisc {
private:
string name;
int mathScore;
}該類別內外皆可存取
外部程式可直接存取、修改
只能在該類別內存取
外部程式無法直接存取,必須用公有函式存取
public
private
class zsisc {
public:
string name;
int height;
}class zsisc {
private:
string name;
int mathScore;
}該類別內外皆可存取
外部程式可直接存取、修改
只能在該類別內存取
外部程式無法直接存取,必須用公有函式存取
| struct | class | |
|---|---|---|
| 預設 | public | private |
| 繼承 | X | O |
| 封裝 | 弱 | 強 |
| 物件導向 | 少 | 多 |
| struct | class | |
|---|---|---|
| 預設 | public | private |
| 繼承 | X | O |
| 封裝 | 弱 | 強 |
| 物件導向 | 少 | 多 |
struct----簡單資料結構
class ----物件導向
可將不同資料型態同時處存
#include <bits/stdc++.h>
using namespace std;
struct scoreList {
string name;
double englishScore;
float chineseScore;
int mathScore;
void avg() {
cout << (englishScore + mathScore + chineseScore) / 3 << endl;
}
};
int main() {
// 賦值
scoreList student = {"Amy", 59.99, 79.9, 60};
student.avg();
}可將不同資料型態同時儲存
注意:在主程式之外!
#include <bits/stdc++.h>
using namespace std;
struct scoreList {
string name;
double englishScore;
float chineseScore;
int mathScore;
void avg() {
cout << (englishScore + mathScore + chineseScore) / 3 << endl;
}
};
int main() {
// 賦值
scoreList student = {"Amy", 59.99, 79.9, 60};
student.avg();
}struct
struct id{
int num;
string name;
};
struct checkup{
id studentNumber;
int grade;
int class;
int number;
};struct Grade {
string name;
int score;
};
Grade student[3] = {
{"72", 60},
{"73", 50},
{"74", 90}
};
struct
struct可以放在struct裡
struct id{
int num;
string name;
};
struct checkup{
id studentNumber;
int grade;
int class;
int number;
};struct在陣列
struct Grade {
string name;
int score;
};
Grade student[3] = {
{"72", 60},
{"73", 50},
{"74", 90}
};
Dynamic programming
動態規劃
Dp - 定義
大問題
小問題
小問題
小問題
1. 最優子結構
問題的最優解可以由其子問題的最優解構成.
2. 重疊子問題
不同問題在求解過程中會包含重複的子問題 (透過記憶化或表格法可以避免重複計算).
3. 無後效性
當一個子問題的解確定後, 後續計算不會影響該解的正確性.
提升效率 !!!

Dp - 定義
Dp - Greedy VS. DP
海綿寶寶今天要去 拌咖哩國 與 不拌咖哩國 旅遊, 他想要在兩個國家都分別買一個15元的咖哩蟹堡, 請幫他想想該如何付錢吧~
拌咖哩國
不拌咖哩國
1
5
10
1
5
11

咖哩拌不拌不重要
我們來吃咖哩蟹堡 !
Dp - Greedy VS. DP
拌咖哩國
不拌咖哩國
Greedy
DP
我要一15元的咖哩蟹堡 !!
1
5
10
5
10
11
1
1
1
5
5
5
1
5
10
1
5
11
Dp - 概念
設 f(x) 為價值 x 元的商品所需要的最少硬幣數
11
如果付
f(15) = f(4) + 1
如果付
f(15) = f(10)+ 1
5
如果付
1
f(x) = min{ f(x-11), f(x-5), f(x-1) } + 1
f(15) = min{ f(4), f(10), f(14) } + 1
f(15)
f(4)
f(10)
f(14)
.
.
.
.
.
.
.
.
.
f(15) = f(14)+ 1
Dp - 費氏數列
* f(n) = f(n−1) + f(n−2) (n≥2)
#include<iostream>
using namespace std;
long long fib( long long num ){
long long dp[num + 1];
dp[0] = 0;
dp[1] = 1;
for(int i=2; i<num+1; i++){
dp[i] = dp[i-1] + dp[i-2];
}
return dp[num];
}
int main(){
long long num = 0;
cin >> num;
cout << fib(num) << endl;
return 0;
}使用陣列記憶化
Dp - 路徑問題
#include<bits/stdc++.h>
using namespace std;
int main() {
int grid[3][4] = {
{0, 7, 8, 9},
{1, 2, 5, 1},
{1, 4, 10, 0}
};
int dp[3][4];
dp[0][0] = grid[0][0];
for (int i=1; i<4; i++) {
dp[0][i] = dp[0][i - 1] + grid[0][i];
}
for (int i=1; i<3; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (int i=1; i<3; i++) {
for (int j = 1; j < 4; j++) {
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
cout << "最短路徑總和為:" << dp[2][3] << endl;
return 0;
}
使用陣列記憶化
空間複雜度 / 時間複雜度
複雜度 - 定義
1. 時間複雜度
定性描述該演算法的執行時間
2. 空間複雜度
定性地描述該演算法或程式執行所需要的儲存空間大小
複雜度 - 時間複雜度
基礎運算(宣告、賦值、運算...)皆為一單位時間
int a;
a = 5;
a = a + 3;T(n) = 3
BUT !! 實際運算時不需要那麼詳細的數值
複雜度 - 時間複雜度
使用大O符號( O(1) 、O(n)、O(n²)... )表示時間複雜度
- 忽略低次項與常數項
- 聚焦於最壞情況
忽略低次項
忽略常數項
O(n+1) → O(n)
O(20n²) → O(n²)
O(n²+n) → O(n²)
O(nlog(n)+n) → O(nlog(n))
→ 描述一個演算法在輸入 n 個東西時, 總執行時間與 n 的關係.
複雜度 - 時間複雜度
常用的空間複雜度與演算法
O(1):陣列讀取
O(n):簡易搜尋(一層迴圈)
O(log n):二分搜尋
O(nlogn):合併排序
O(n²):選擇排序(兩層迴圈)
O(2^n):費波那契數列

複雜度 - 空間複雜度
大部分的原始型別(數字、布林值...)都是固定的空間
→ O(1)
字串
→ O(n) (n為字串長度)
物件型別的陣列與物件
→ O(n) (n為陣列的長度或是物件的 key 數量)
複雜度 - 空間複雜度
int i;
int a[n];
int b[n][n]S(n)=n²+n+8=O(n² )
C++ Review
By zsisc32
C++ Review
- 67

